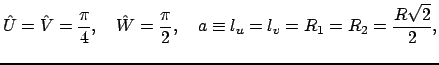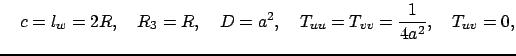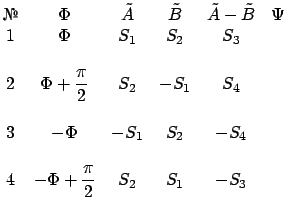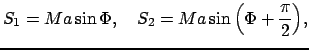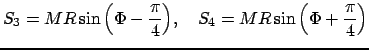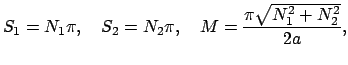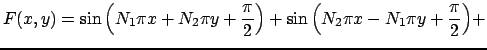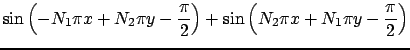

Next: Требуется аннотация на английском
Up: Построение карты рассчитанных треугольников
Previous: Серия 2.
Равнобедренный прямоугольный треугольник имеет пропорцию углов 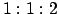 . Вычислим его константы, считая заданным
. Вычислим его константы, считая заданным 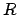 .
.
Число углов 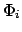 равно 4. Каждое частное решение
равно 4. Каждое частное решение 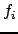 формируется из строки следующей матрицы
, где
формируется из строки следующей матрицы
, где
Имеем далее
и решение имеет следующий вид
, где 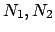 - целые числа, а
- целые числа, а 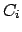 округляются по
округляются по 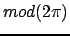 :
:
Поскольку для равнобедренного прямоугольного треугольника можно отождествить координаты 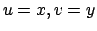 , далее приведён пример решения в переменных
, далее приведён пример решения в переменных 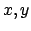
Фунция 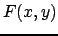 есть собственная функция уравнения (1), где
есть собственная функция уравнения (1), где
, 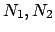 - произвольные целые числа, а треугольник
- произвольные целые числа, а треугольник
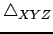 имеет координаты
имеет координаты
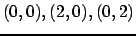 .
.


Next: Требуется аннотация на английском
Up: Построение карты рассчитанных треугольников
Previous: Серия 2.
Бродников А.П.
2006-04-16
Используются технологии
uCoz![]() . Вычислим его константы, считая заданным
. Вычислим его константы, считая заданным ![]() .
.