Метод цепных дробей

Постановка задачи: найти приближения вещественного числа $\alpha$ рациональнымы, желательно с наилучшей в некотором смысле точностью. Например, чтобы абсолютная ошибка ${\left\vert{}a/b - \alpha\right\vert}$ не превышала ${1/b}$, где ${a,b \in Z}$. Если $\alpha \in Z$, приближение единственно: $\alpha/1$. Иначе запускается следующий шаговый алгоритм:

1. Задать аргументы: $\alpha$ - приближаемое число, $n$ - максимальное число итераций. Создать массивы $\alpha_i$ - массив частных, и $a_i$ - массив неполных частных. Переход на шаг 2;

2. $\alpha_0 := \alpha; i := 0;$ ($i$ - число выполненных итераций); Переход на шаг 3;

3. $a_i := \left\lfloor\alpha_i\right\rfloor\;$ Переход на шаг 4;

4. Если ${\alpha_i-a_i = 0}$, то выход, иначе переход на шаг 5;

5. Если $i + 1 > n$, то выход, иначе переход на шаг 6;

6. 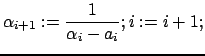${\alpha_{i+1} := \displaystyle\frac{1}{\alpha_i-a_i}; i := i + 1;}$ Переход на шаг 3.

В результате получаем для $\alpha$ выражение в виде

$$\alpha = a_0 + \frac{1}{\displaystyle a_1 + \frac{1}{\displaystyle a_2 + \frac{1}{\displaystyle a_3 + \ldots}}}$$

, которое принято записывать в линию примерно так:

$$\alpha = a_0 + \frac{\scriptstyle{1\lefteqn{/}}}{\phantom{}}\:a_1... ...hantom{}}\:a_2 + \frac{\scriptstyle{1\lefteqn{/}}}{\phantom{}}\:a_3 + \ldots$$

Если $\alpha\in{Q}$, то ряд состоит из конечного числа слагаемых. Для иррациональных $\alpha$ ряд бесконечен и всегда сходится к $\alpha$. У цепных дробей числители равны $1$, у непрерывных дробей числители - произвольны.

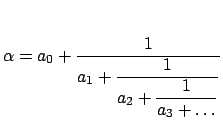
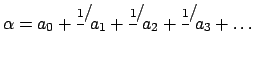
Конечная сумма вида 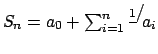${ S_n = a_0 + \sum_{i=1}^n\frac{\scriptstyle{1\lefteqn{/}}}{\phantom{}}\:a_i }$ называется $n$-й подходящей дробью и является рациональным числом. Существуют рекуррентные формулы для вычисления таких сумм, которые естественно обобщаются на случай цепных пропорций.

Используются технологии uCoz