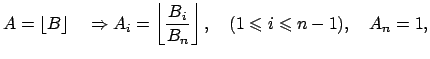

Next: Разложение пропорции в цепную
Up: propor
Previous: Пропорции
На множестве пропорций определены бинарные операции пропорционального сложения 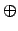 и пропорционального вычитания
и пропорционального вычитания 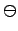 . Пусть
. Пусть
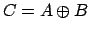 , где
, где 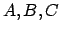 - пропорции размера
- пропорции размера 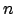 . Тогда
. Тогда
Если
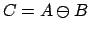 , то
, то
В отличие от дробей, последний компонент пропорции, к примеру, 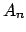 , может принимать значение 0. Верны формулы
, может принимать значение 0. Верны формулы
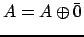 и
и
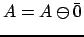 .
.
Бинарные операции сравнения
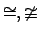 на множестве пропорций возвращают логический результат
на множестве пропорций возвращают логический результат 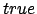 или
или 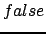 . Операция
. Операция 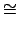 определяется на паре пропорций
определяется на паре пропорций 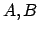 следующим образом:
следующим образом:
Операция 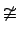 возвращает противоположный признак результата, нежели
возвращает противоположный признак результата, нежели 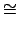 .
.
На множестве пропорций определена унарная операция инверсия 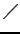 . В случае
. В случае 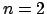 ей соответствует операция обращения дроби, когда числитель и знаменатель меняются местами. В отличие от обычной дроби знаменатель пропорции может принимать значение 0. В случае
ей соответствует операция обращения дроби, когда числитель и знаменатель меняются местами. В отличие от обычной дроби знаменатель пропорции может принимать значение 0. В случае 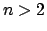 инверсия пропорции - это просто некоторая перестановка, отличная от тождественной, её компонентов. Более строгие правила правила могут требовать отсутствия циклов либо налагать какие-либо иные ограничения на эту перестановку. В данном случае вполне достаточно объявить инверсией перестановку циклического сдвига влево:
инверсия пропорции - это просто некоторая перестановка, отличная от тождественной, её компонентов. Более строгие правила правила могут требовать отсутствия циклов либо налагать какие-либо иные ограничения на эту перестановку. В данном случае вполне достаточно объявить инверсией перестановку циклического сдвига влево:
Операция, обратная инверсии, обозначается символом 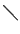 . Это есть перестановка циклического сдвига вправо:
. Это есть перестановка циклического сдвига вправо:
На множестве пропорций определена унарная операция 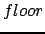 . Записывается она для пропорций
. Записывается она для пропорций 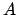 и
и 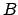 так:
так:
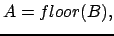 либо либо 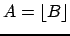 |
|
, что означает


Next: Разложение пропорции в цепную
Up: propor
Previous: Пропорции
Бродников А.П.
2006-04-19
Используются технологии
uCoz