
Next: About this document ...
Up: propor
Previous: Операции над пропорциями
Обозначим через
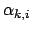
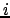 -ю компоненту пропорции
-ю компоненту пропорции 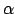 на
на 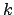 -том шаге итерации. Соответственно
-том шаге итерации. Соответственно 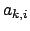 - это
- это 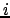 -я компонента пропорции
-я компонента пропорции 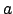 на
на 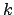 -том шаге итерации.
-том шаге итерации.
Для произвольной пропорции 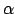 алгоритм разложения её в цепную пропорцию выглядит следующим образом:
алгоритм разложения её в цепную пропорцию выглядит следующим образом:
1. Задать аргументы 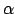 - приближаеиая пропорция,
- приближаеиая пропорция, 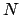 - максимальное
число итераций. Создать массив
- максимальное
число итераций. Создать массив 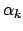 - массив частных пропорций и
- массив частных пропорций и 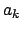 - массив неполных частных пропорций. Переход на шаг 2.
- массив неполных частных пропорций. Переход на шаг 2.
2.
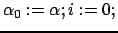 (
(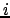 - число выполненных итераций); Переход на шаг 3;
- число выполненных итераций); Переход на шаг 3;
3.
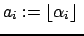 Переход на шаг 4.
Переход на шаг 4.
4. Вычислить пропорцию
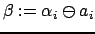 . Если
. Если
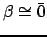 , то выход. Иначе переход на шаг 5;
, то выход. Иначе переход на шаг 5;
5. Если 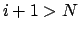 , то выход, иначе переход на шаг 6;
, то выход, иначе переход на шаг 6;
6.
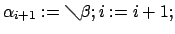 Переход на шаг 3.
Переход на шаг 3.
В результате получаем для 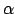 выражение вида
выражение вида
, которое можно записать в линию примерно так:
Конечная сумма вида
называется 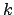 -й подходящей пропорцией, она эквивалентна некоторой рациональной пропорции, так как имеет представление, все компоненты которого целочисленны. Знак
-й подходящей пропорцией, она эквивалентна некоторой рациональной пропорции, так как имеет представление, все компоненты которого целочисленны. Знак 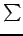 здесь означает последовательное применение операции пропорционального сложения
здесь означает последовательное применение операции пропорционального сложения 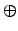 . Для рациональной пропорции процесс разлодения в цепную будет конечным, так как целые числа частных пропорций
. Для рациональной пропорции процесс разлодения в цепную будет конечным, так как целые числа частных пропорций
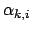 убывают.
убывают.
Приведём пример разложения пропорции в цепную пропорцию. Пусть
![$ \alpha=(\sqrt[3]{4}:\sqrt[3]{2}:1)'$](img72.png) , где
, где 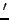 - знак траспозиции. Тогда
- знак траспозиции. Тогда
Поскольку
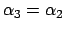 , при дальнейшем разложении пропорции
, при дальнейшем разложении пропорции 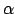 неполные частные
неполные частные 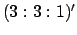 будут повторяться, т.е. разложение пропорции, составленной из алгебраических чисел, или модуля -
будут повторяться, т.е. разложение пропорции, составленной из алгебраических чисел, или модуля -
![$ (\sqrt[3]{4}:\sqrt[3]{2}:1)'$](img82.png) является периодическим, и, следовательно, бесконечным.
является периодическим, и, следовательно, бесконечным.
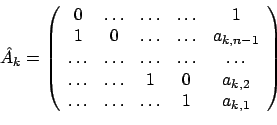
Займёмся рекуррентными формулами для вычисления компонент подходящих пропорций. Определим квадратную матрицу 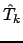 размера
размера 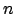 , составленную из столбцов
, составленную из столбцов
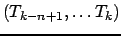 . Стартовой матрицей будет матрица
. Стартовой матрицей будет матрица
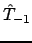 , заполненная числами 0 повсюду, за исключением побочной диагонали, содержащей числа
, заполненная числами 0 повсюду, за исключением побочной диагонали, содержащей числа 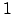 .
Вектор-столбец
.
Вектор-столбец 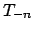 имеет значение
имеет значение
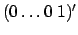 , а вектор-столбец
, а вектор-столбец 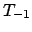 , соответственно,
, соответственно,
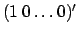 . Обозначим
. Обозначим
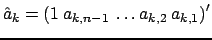 и выпишем таблицу, где верхняя строка содержит номер итерации при вычислении цепной пропорции.
и выпишем таблицу, где верхняя строка содержит номер итерации при вычислении цепной пропорции.
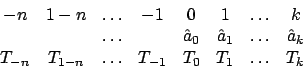 |
(1) |
Теперь получить формулу
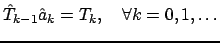 |
(2) |
по индукции несложно. Именно эта формула (2) используется для вычисления вектор-столбца 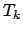 , который является представлением
, который является представлением 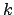 -той подходящей пропорции. Если ввести в рассмотрение матрицу, где все незаполненные элементы равны 0,
, то формулу (2) можно записать в матричном виде
-той подходящей пропорции. Если ввести в рассмотрение матрицу, где все незаполненные элементы равны 0,
, то формулу (2) можно записать в матричном виде
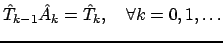 |
(3) |
Полезность такой записи состоит в том, что
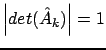 ,
,
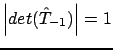 , и, следовательно,
, и, следовательно,
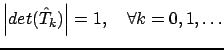 |
(4) |
Поскольку в (1) все матрицы 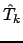 целочисленны, (4) означает, что любая из них целочисленно обратима, т.е.
целочисленны, (4) означает, что любая из них целочисленно обратима, т.е.
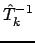 - тоже целочисленная матрица. Имея
- тоже целочисленная матрица. Имея
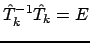 , мы немедленно получаем
, мы немедленно получаем
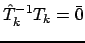 . Получить такой результат без метода цепных пропорций было бы весьма непросто.
. Получить такой результат без метода цепных пропорций было бы весьма непросто.
Последнему результату можно придать и другую, имеющую большое практическое применение, формулировку. Пусть
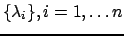 - последовательность целых чисел, такая, что Н.О.Д
- последовательность целых чисел, такая, что Н.О.Д
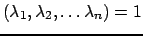 . Тогда существует целочисленное линейное преобразование с детерминантом, по модулю равном
. Тогда существует целочисленное линейное преобразование с детерминантом, по модулю равном 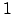 , переводящее линейную комбинацию
, переводящее линейную комбинацию
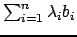 в
в
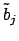 . Здесь переменные
. Здесь переменные 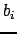 - переменные до преобразования,
- переменные до преобразования,
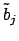 - после. Индекс
- после. Индекс 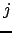 - произволен. Для построения такого преобразования достаточно вектор из чисел
- произволен. Для построения такого преобразования достаточно вектор из чисел 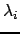 , переставленных в зависимости от
, переставленных в зависимости от 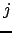 порядке, записать в виде пропорции и разложить эту пропорцию в цепную пропорцию. Разложение будет конечным и оборвётся на некотором шаге
порядке, записать в виде пропорции и разложить эту пропорцию в цепную пропорцию. Разложение будет конечным и оборвётся на некотором шаге 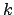 , так как числа
, так как числа 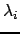 - целые. Матрица
- целые. Матрица
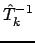 будет искомой матрицей преобразования. Далее показан простой способ её вычисления.
будет искомой матрицей преобразования. Далее показан простой способ её вычисления.
Из (3) следует
, что позволяет, зная
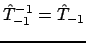 и
и
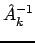 , рекуррентно вычислить
, рекуррентно вычислить
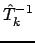 , проводя все вычисления в целых числах.
Матрица
, проводя все вычисления в целых числах.
Матрица
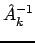 имеет вид
, где все незаполненные элементы равны 0. Умножение этой матрицы на любую другую не представляет никакой сложности из-за регулярности её структуры и разрежённости.
имеет вид
, где все незаполненные элементы равны 0. Умножение этой матрицы на любую другую не представляет никакой сложности из-за регулярности её структуры и разрежённости.
Несложно показать, что если разложение некоторой пропорции 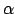 в цепную пропорцию имеет период, то
в цепную пропорцию имеет период, то 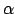 - алгебраический модуль, т.е. вектор, составленный из алгебраических чисел степени не выше
- алгебраический модуль, т.е. вектор, составленный из алгебраических чисел степени не выше 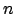 . Если некоторые частные пропорции эквивалентны друг другу, т.е.
. Если некоторые частные пропорции эквивалентны друг другу, т.е.
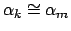 , то существует целочисленная матрица
, то существует целочисленная матрица 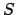 с детерминантом, равным
с детерминантом, равным 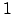 или
или 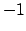 , такая, что
, такая, что
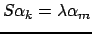 . Тогда
. Тогда
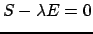 , откуда легко следует нужный результат. Сама матрица
, откуда легко следует нужный результат. Сама матрица 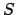 вычисляется по матрицам
вычисляется по матрицам  , упражнение для студентов.
, упражнение для студентов.


Next: About this document ...
Up: propor
Previous: Операции над пропорциями
Бродников А.П.
2006-04-19
Используются технологии
uCoz![]() - приближаеиая пропорция,
- приближаеиая пропорция, ![]() - максимальное
число итераций. Создать массив
- максимальное
число итераций. Создать массив ![]() - массив частных пропорций и
- массив частных пропорций и ![]() - массив неполных частных пропорций. Переход на шаг 2.
- массив неполных частных пропорций. Переход на шаг 2.
![]() (
(![]() - число выполненных итераций); Переход на шаг 3;
- число выполненных итераций); Переход на шаг 3;
![]() Переход на шаг 4.
Переход на шаг 4.
![]() . Если
. Если
![]() , то выход. Иначе переход на шаг 5;
, то выход. Иначе переход на шаг 5;
![]() , то выход, иначе переход на шаг 6;
, то выход, иначе переход на шаг 6;
![]() Переход на шаг 3.
Переход на шаг 3.
![]() выражение вида
выражение вида
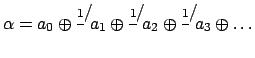
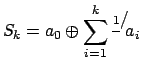
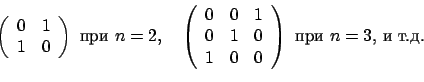
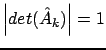 ,
,
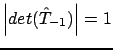 , и, следовательно,
, и, следовательно,