Постановка задачи

Требуется найти решение уравнения Гельмгольца

$$\Delta F=-M^2F, \Delta=\nabla^2=\frac{\partial^2}{\partial{x^2}}+\frac{\partial^2}{\partial{y^2}}$$ (1)

, при следующих граничных условиях:

$$F\bigl\vert _\Gamma=0 \mbox{на границе треугольной области $\Gamma$}$$ (2)

Решение существует только для определённых значений 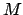$M$, которые называются собственными числами. Конкретная функция 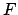$F$ для некоторого значения 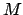$M$ называется собственной функцией, соответствующей этому значению.

Общее решение (1) можно записать в виде:

$$F(x,y)=\int_0^{2\pi}\Omega(\theta)\sin{\{M(x)\cos{\theta}+y\sin{\theta}+\chi(\theta)\}}d\theta$$ (3)

, где $\Omega(\theta),\chi(\theta)$ - обобщённые функции.

Используются технологии uCoz