

Next: Серия 2.
Up: Равносторонний треугольник
Previous: Равносторонний треугольник
Подберём 3 таких угла 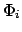 , чтобы
, чтобы
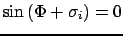 и составим таблицу всего из трёх строк, соответствующим этим углам. Напоминаем, что каждое частное решение, соответствующее
и составим таблицу всего из трёх строк, соответствующим этим углам. Напоминаем, что каждое частное решение, соответствующее 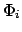 , имеет вид
, имеет вид
, где
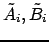 вычисляются через
вычисляются через 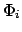 .
.
Запишем матрицу из коэффициентов частных решений
, а затем начнём заполнять пустые места, вычисляя значения
Здесь была использована формула
В каждом из столбцов
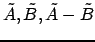 легко находятся пары с совпадающими либо противоположными по знаку значениями. Из пары
легко находятся пары с совпадающими либо противоположными по знаку значениями. Из пары
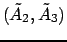 , используя (19) и полагая
, используя (19) и полагая
, получаем
Из пары
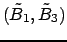 , используя (19) и полагая
, используя (19) и полагая
, получаем
Наконец, из пары
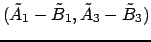 , используя (18) и полагая
, используя (18) и полагая
, получаем
, где
 ,
,
 .
.
Коэффициенты 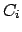 , с одной стороны, имеют значения
, с одной стороны, имеют значения 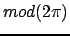 ; с другой стороны, позволяя им принимать значения при различных
; с другой стороны, позволяя им принимать значения при различных 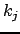 , можно получить весь ряд собственных чисел и собственных значений. Поэтому сначала берутся во внимание их общие значения, до вычисления
, можно получить весь ряд собственных чисел и собственных значений. Поэтому сначала берутся во внимание их общие значения, до вычисления 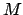 в виде функции от целочисленных индексов
в виде функции от целочисленных индексов 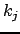 , затем эти значения обрезаются по
, затем эти значения обрезаются по 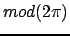 без потери общности.
без потери общности.
Выпишем выражение для 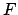 полностью.
полностью.
Полагая в (29)
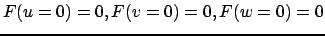 , получим остальные зависимости для
, получим остальные зависимости для 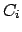
Отсюда несложно получить
и от остальных 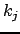 можно отказаться, а
можно отказаться, а 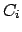 - обрезать по
- обрезать по 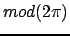 . Выделим выражение для
. Выделим выражение для 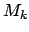
, здесь 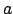 - длина стороны равностороннего треугольника.
- длина стороны равностороннего треугольника.
Для 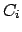 возможны два варианта решения
возможны два варианта решения
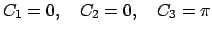 |
(30) |
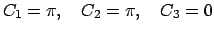 |
(31) |
В случае (30) решение записывается в виде
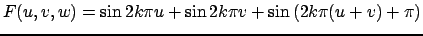 |
(32) |
В случае (31) решение отличается только множителем, что для собственных функций несущественно. Отметим ещё несколько эквивалентных выражений для решения
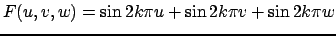 |
(33) |
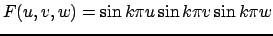 |
(34) |
Выражение (33) является аддитивной функцией трёх синусов, а (34) - мультипликативной функцией трёх синусов.


Next: Серия 2.
Up: Равносторонний треугольник
Previous: Равносторонний треугольник
Бродников А.П.
2006-04-16
Используются технологии
uCoz![]() , чтобы
, чтобы
![]() и составим таблицу всего из трёх строк, соответствующим этим углам. Напоминаем, что каждое частное решение, соответствующее
и составим таблицу всего из трёх строк, соответствующим этим углам. Напоминаем, что каждое частное решение, соответствующее ![]() , имеет вид
, имеет вид
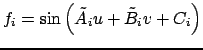
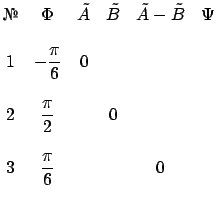
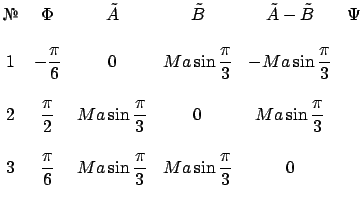
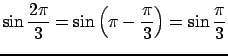
![]() , с одной стороны, имеют значения
, с одной стороны, имеют значения ![]() ; с другой стороны, позволяя им принимать значения при различных
; с другой стороны, позволяя им принимать значения при различных ![]() , можно получить весь ряд собственных чисел и собственных значений. Поэтому сначала берутся во внимание их общие значения, до вычисления
, можно получить весь ряд собственных чисел и собственных значений. Поэтому сначала берутся во внимание их общие значения, до вычисления ![]() в виде функции от целочисленных индексов
в виде функции от целочисленных индексов ![]() , затем эти значения обрезаются по
, затем эти значения обрезаются по ![]() без потери общности.
без потери общности.
![]() полностью.
полностью.
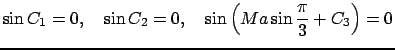
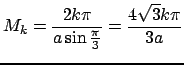
![]() возможны два варианта решения
возможны два варианта решения