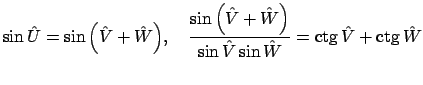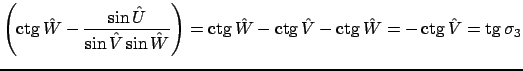

Next: Стратегия построения решения
Up: start
Previous: Правила учёта граничных условий
Перепишем левую часть (14) в виде
![$\displaystyle T_{uu}\tilde A^2+T_{vv}\tilde B^2+2T_{uv}\tilde A\tilde B\equiv T...
...ilde B^2- 2\frac{\sin{\hat V}\cos{\hat W}}{\sin{\hat U}}\tilde A\tilde B\right]$](img87.png) |
(20) |
Продолжая, имеем
, где
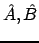 и
и
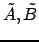 связаны зависимостями
связаны зависимостями
Тогда
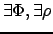 такие, что
такие, что
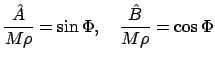 |
(21) |
и верны
, удовлетворяющие уравнению (7).
Такой угол 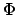 будем называть решающим углом уравнений (21),
(14), принадлежашим данному частному решению.
будем называть решающим углом уравнений (21),
(14), принадлежашим данному частному решению.
Приведём 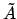 к более удобному виду
к более удобному виду
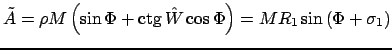 |
(22) |
В (22) 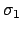 должно удовлетворять
должно удовлетворять
поэтому
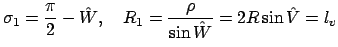 |
(23) |
Для 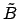 имеем
имеем
, где
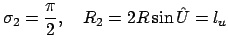 |
(24) |
Для
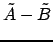 имеем
имеем
Поскольку
, то для
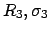 имеем
имеем
, где из двух вариантов для 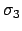 выбран тот, который задаёт правильный знак согласно (8).
выбран тот, который задаёт правильный знак согласно (8).


Next: Стратегия построения решения
Up: start
Previous: Правила учёта граничных условий
Бродников А.П.
2006-04-16
Используются технологии
uCoz![$\displaystyle T_{uu}\tilde A^2+T_{vv}\tilde B^2+2T_{uv}\tilde A\tilde B\equiv T...
...ilde B^2- 2\frac{\sin{\hat V}\cos{\hat W}}{\sin{\hat U}}\tilde A\tilde B\right]$](img87.png)
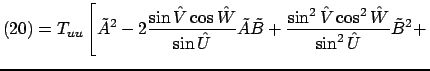
![$\displaystyle \left.\frac{\sin^2{\hat V}}{\sin^2{\hat U}}\left(1-\cos^2{\hat W}\right)\tilde B^2 \right] \notag$](img89.png)
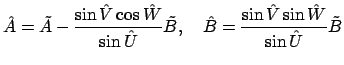
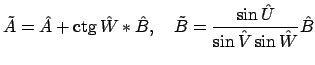
![]() будем называть решающим углом уравнений (21),
(14), принадлежашим данному частному решению.
будем называть решающим углом уравнений (21),
(14), принадлежашим данному частному решению.
![]() к более удобному виду
к более удобному виду
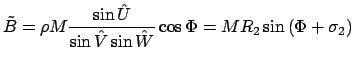
![$\displaystyle \tilde A-\tilde B=\rho M\left[\sin{\Phi}+\left(\ctg{\hat W}-\frac{\sin{\hat U}}{\sin{\hat V}\sin{\hat W}} \right)\cos{\Phi} \right]=$](img110.png)
![$\displaystyle \rho M\left(\sin{\Phi}-\ctg{\hat V}\cos{\Phi}\right)= \rho M\left[\sin{\Phi}+\tg{\left(\frac{3\pi}{2}+\hat V\right)}\cos{\Phi}\right]=$](img111.png)