

Next: Серия 1.
Up: Построение карты рассчитанных треугольников
Previous: Построение карты рассчитанных треугольников
Равносторонний треугольник - это одновременно равноугольный треугольник, ему соответствует пропорция углов  . Имеет две серии решений. Вычислим его константы, считая заданным
. Имеет две серии решений. Вычислим его константы, считая заданным 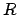 .
.
Subsections
Бродников А.П.
2006-04-16
Используются технологии
uCoz![]() . Имеет две серии решений. Вычислим его константы, считая заданным
. Имеет две серии решений. Вычислим его константы, считая заданным ![]() .
.

