

Next: Равнобедренный прямоугольный треугольник
Up: Равносторонний треугольник
Previous: Серия 1.
Число углов 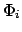 равно 6. Каждое частное решение
равно 6. Каждое частное решение 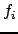 формируется из строки следующей матрицы
, где
формируется из строки следующей матрицы
, где
Выпишем совокупность полученных уравнений, связывающих свободные члены частных решений
Поскольку
, то (37) следует переписать в виде
Для решения достаточно положить
, где 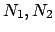 - целые числа, и тогда
- целые числа, и тогда
Вычисляя (13) для каждого слагаемого в (41), убеждаемся в том, что
Здесь  являются соответственно семейством собственных функций и семейством собственных значений, зависящих от целочисленных параметров
являются соответственно семейством собственных функций и семейством собственных значений, зависящих от целочисленных параметров 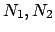 .
.


Next: Равнобедренный прямоугольный треугольник
Up: Равносторонний треугольник
Previous: Серия 1.
Бродников А.П.
2006-04-16
Используются технологии
uCoz








