Вид решения

Учитывая (1), (3), (9) и (10), общее решение ${F}$ будем искать в виде суммы частных решений ${f_i}$

$$F=\sum\limits^n_{i=1}{f_i(u,v,w)}$$ (11)

, где каждая частная функция ${f_i}$ имеет вид

$$f_i(u,v,w)=\sin\!{(A_iu+B_iv+C_iw)}$$ (12)

Опуская нижние индексы в (12), выполним замены

$$\tilde A=A-C,\quad\tilde B=B-C$$

, затем, выбрав в качестве независимых $T_{uu},T_{vv},T_{uv}$, и используя (5), линейность лапласиана $\Delta$, упростим формулы:

$$f=\sin\!{(\tilde Au+\tilde Bv+C)}$$

$$\Delta f\equiv -(T_{uu}\tilde A^2+T_{vv}\tilde B^2+2T_{uv}\tilde A\tilde B)f=-M^2f$$ (13)

Сокращая (13) на $f$, получаем

$$T_{uu}\tilde A^2+T_{vv}\tilde B^2+2T_{uv}\tilde A\tilde B=M^2$$ (14)

Каждая частная функция 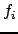$f_i$ удовлетворяет линейному уравнению (9) самостоятельно, сумма же их, равная 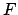$F$, должна удовлетворять граничным условиям (10).

Используются технологии uCoz