

Next: Построение карты рассчитанных треугольников
Up: start
Previous: Приведённый вид частного уравнения
Пусть  - частное решение уравнения (1), имеющее вид (12),
- частное решение уравнения (1), имеющее вид (12),  -е слагаемое ряда (11)
-е слагаемое ряда (11)
Уравнение (25) не удовлетворяет совокупности граничных условий (15), (16),
(17) хотя бы потому, что не существует такого  , чтобы одновременно выполнялись равенства
, чтобы одновременно выполнялись равенства
Следовательно, если и существует решение в виде суммы (11), это должна быть сумма нескольких слагаемых. Чтобы подавить ненулевое слагаемое
 ,
нужно подобрать такой угол
,
нужно подобрать такой угол
 , чтобы либо
, чтобы либо
 |
(26) |
, либо
 |
(27) |
В случае (26) используется правило (19), где
 |
(28) |
В случае (27) используется правило (18) с той же формулой (28).
Для подавления
 используется та же формула (28) с заменой
используется та же формула (28) с заменой 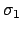 на
на  .
Для подавления
.
Для подавления
 используется та же формула (28) с заменой
используется та же формула (28) с заменой 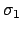 на
на 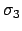 ,
,  на
на
 ,
,
 на
на
 .
.
Правила (18) и (19) приводят к системе линейных уравнений, которая будет совместной только при определённых значениях 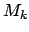 . Но решать такую систему современная математика умеет только в случае её конечности. Для конкретного
. Но решать такую систему современная математика умеет только в случае её конечности. Для конкретного
 и любого
и любого
 несложно найти такой
несложно найти такой
 , чтобы подавить один из
, чтобы подавить один из
 , а тогда появятся неподавленные слагаемые для
, а тогда появятся неподавленные слагаемые для
 . Для произвольного
. Для произвольного
 , с любыми углами
, с любыми углами
 процесс бесконечен, но если хотя бы два из углов треугольника рационально эквивалентны
процесс бесконечен, но если хотя бы два из углов треугольника рационально эквивалентны  ,
то процесс добавления
,
то процесс добавления
 заканчивается на некотором шаге. Это есть следствие периодичности тригонометрических функций. Угол
заканчивается на некотором шаге. Это есть следствие периодичности тригонометрических функций. Угол  рационально эквивалентен
рационально эквивалентен  , если существуют такие целые числа
, если существуют такие целые числа  , что
, что
Ввиду (6) третий угол
 также рационально эквивалентен
также рационально эквивалентен  , если это свойство выполняется для двух других углов.
, если это свойство выполняется для двух других углов.
Вычислим  - максимальное число слагаемых. Пусть целые числа
- максимальное число слагаемых. Пусть целые числа
 таковы, что
таковы, что
, где Н.О.Д - наименьший общий делитель, а Н.О.К - наименьшее общее кратное.
Тогда
Число  появляется из-за знаменателя
появляется из-за знаменателя
 в (23), (24),
(25).
Формулы для вычисления углов треугольника
в (23), (24),
(25).
Формулы для вычисления углов треугольника
Зная углы, можно вычислить их синусы, а зная 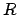 , вычислить стороны и тем самых полностью построить
, вычислить стороны и тем самых полностью построить
 .
.


Next: Построение карты рассчитанных треугольников
Up: start
Previous: Приведённый вид частного уравнения
Бродников А.П.
2006-04-16
Используются технологии
uCoz
![]() . Но решать такую систему современная математика умеет только в случае её конечности. Для конкретного
. Но решать такую систему современная математика умеет только в случае её конечности. Для конкретного
![]() и любого
и любого
![]() несложно найти такой
несложно найти такой
![]() , чтобы подавить один из
, чтобы подавить один из
![]() , а тогда появятся неподавленные слагаемые для
, а тогда появятся неподавленные слагаемые для
![]() . Для произвольного
. Для произвольного
![]() , с любыми углами
, с любыми углами
![]() процесс бесконечен, но если хотя бы два из углов треугольника рационально эквивалентны
процесс бесконечен, но если хотя бы два из углов треугольника рационально эквивалентны ![]() ,
то процесс добавления
,
то процесс добавления
![]() заканчивается на некотором шаге. Это есть следствие периодичности тригонометрических функций. Угол
заканчивается на некотором шаге. Это есть следствие периодичности тригонометрических функций. Угол ![]() рационально эквивалентен
рационально эквивалентен ![]() , если существуют такие целые числа
, если существуют такие целые числа ![]() , что
, что
